By Helen Hill for MGHPCC
The potential for loss of property and life, has made earthquake forecasting and prediction an active area of research for statisticians and earth scientists. While it is not currently possible to make deterministic predictions of when and where earthquakes will happen, new techniques like those recently reported by the Meade Group in the Department of Earth and Planetary Sciences at Harvard using computers housed at the MGHPCC, bring closer the day when the behavior of a seismically active region can me modeled quickly enough to be able to provide meaningful lifesaving guidance to at risk populations.
According to our familiar picture of the Earth, our planet is a ~6400 km thick planet comprising a metalic core surrounded by a rocky ~3000 km deep layer (the mantle) topped by a thin ~5-70km solid outer layer (the crust.)
That crust is broken into a jigsaw of pieces called plates. Heat produced by radioactive decay within the mantle causes it to convect, and the plates floating on it to move. Earthquakes occur where plate boundaries collide and grind past one another. Probably the most famous one, at least for North Americans, is the San Andreas Fault running through California at the boundary between the Pacific and North American plates.
Our commonest experience of rock is that it is an inviolable solid. However, as rocks become hotter and experience greater pressures at depth they become more ductile. In the lower crust and upper mantle rocks take on the behavior of a viscoelastic material (exhibiting both fluid-like and elastic behaviors) and can elastically deform over the short time scales (minutes) when a quake occurs. This process equilibrates the stresses that triggered the quake through propagation of diffusive fronts that radiate out from and echo within proximity of fault zones for years to decades following large earthquakes. The computational cost of traditional viscoelastic earthquake calculations, which evaluate viscoelastic codes at thousands of times and locations, means studies tend to adopt only a few fixed rheological structures (rock types) and model geometries of limited volume, and examine the predicted time-dependent deformation only over short (<10 years) time periods at a given depth after a large earthquake.
In “Enabling Large-scale Viscoelastic Calculations via Neural Network Acceleration” graduate students Phoebe DeVries and Ben Thompson, working with their advisor Brendan Meade, report successfully training an artificial neural network to reproduce the results of conventional but much more computationally expensive calculations, resulting in an impressive speed up allowing their viscoelastic calculations to be completed in minutes to hours, compared with the millions of CPU hours required to run large-scale viscoelastic calculations with existing codes on the same platform.
Scientists who study earthquakes divide their life cycle into four parts: the time between large earthquakes, the time just before, the time during, and the time after. In part because of the computational resource constraints alluded to above, traditional earthquake cycle models have focused on explaining isolated parts of the earthquake cycle at the cost of explaining observations across the entire cycle. Meade and his team seek to find unified models that can explain the observations across the entire earthquake cycle.
An Artificial Neural Network (ANN) offers an alternative representation of any given modeled system. ANN’s provide a computationaly efficient mapping between inputs and outputs, without the need to continuously, explicitly evaluate all the internal variables. In other words, rather than slavishly having to individually calculate and sequentially iterate individual effects on each variable throughout the domain, by training a neural network to give the same overall result as the model it seeks to copy, it can be used to more quickly predict the solution, accelerating the time to completion for the calculation.

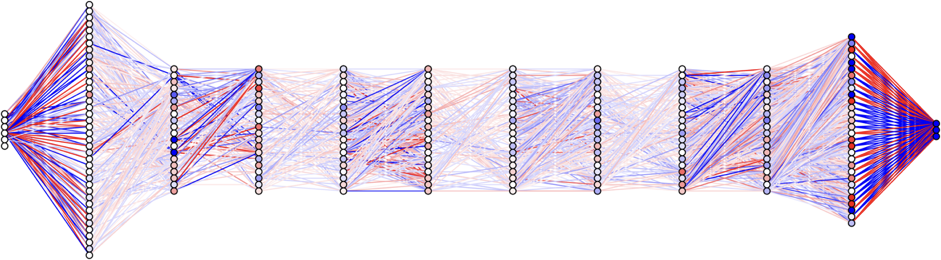Visualization of the structure, weights, and biases of one of the most successful trained ANNs from DeVries et al (2017). The colors of the connections between neurons encode the magnitude and sign (red positive, blue negative) of each individual weight, while the colors of the neurons represent the sign and magnitude of the bias associated with each neuron. The information contained in this visualization (ANN structure, weights, and biases) is, in some sense, a new and compact representation of viscoelastic physics – image courtesy: B. Meade

“What we did was train a compact neural network to learn our physics based viscoelastic earthquake code which previously took 2.5 million CPU hours to run. Now, using our deep neural network, we have been able to perform the same calculations many, many times faster. For instance it now takes only around five hours on an equivalent number of CPUs. This makes practical a world of more complex faults, and a wider range of parameter space to explore, while offering an alternative modeling paradigm with the potential to cut computing overheads by several orders of magnitude,” said Meade. “Besides potentially leading to basic advances in the understanding of the underlying phenomenology, this artificial neural network approach is ripe for use across a range of similarly complex models in the earth sciences, as it can be applied to virtually any physical model, contributing to improved understanding of complicated physical behavior.”
Story image credit: Shutterstock
About the Researcher

Brendan Meade

Brendan Meade is Professor of Earth and Planetary Sciences in the Department of Earth and Planetary Sciences at Harvard. His research is focused on the geodetic imaging of earthquake cycle processes with an emphasis on the detection of interseismic elastic strain accumulation. Meade’s lab is responsible for deconvolving tectonic and earthquake cycle signals across the Japanese Islands to identify the coupled subduction zone interface that ruptured during the great Tohoku-oki earthquake of 2011. He holds Ph.D. in Earth, Atmospheric, and Planetary Sciences from the Massachusetts Institute of Technology and B.A. in the History of Science, Medicine, and Technology from Johns Hopkins University.
Links
Phoebe Robinson DeVries
Ben Thompson
Brendan Meade
Department of Earth and Planetary Sciences, Harvard Faculty of Arts and Sciences
Publication
Phoebe M. R. DeVries,T. Ben Thompson, Brendan J. Meade (2017), Enabling large-scale viscoelastic calculations via neural network acceleration, Geophysical Research Letters, doi: 10.1002/2017GL072716